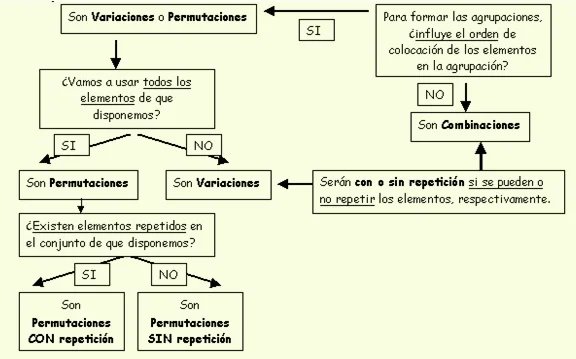
Existen distintas formas de realizar estas agrupaciones, según:
se repitan los elementos o no, según se puedan tomar todos los elementos de que disponemos o no y si influye o no el orden de colocación de los elementos:
Permutaciones sin repetición.
Permutaciones con repetición.
Combinaciones sin repetición.
Combinaciones con repetición.
Las variaciones son aquellas formas de agrupar los elementos de un conjunto teniendo en cuenta que:
- Influye el orden en que se colocan.
- Si permitimos que se repitan los elementos, podemos hacerlo hasta tantas veces como elementos tenga la agrupación.
Existe dos tipos:
- Variaciones SIN repetición
- Variaciones CON repetición
1) ¿De cuántas formas diferentes se pueden cubrir los puestos de presidente, vicepresidente y tesorero de un club de fútbol sabiendo que hay 12 posibles candidatos?
No entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.
![]()
2) Con las letras de la palabra libro, ¿cuántas ordenaciones distintas se pueden hacer que empiecen por vocal?
La palabra empieza por i u o seguida de las 4 letras restantes tomadas de 4 en 4.
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.

3) ¿De cuántas formas pueden mezclarse los siete colores del arco iris tomándolos de tres en tres?
No entran todos los elementos.
No importa el orden.
No se repiten los elementos.

4) ¿Cuántos números de cinco cifras distintas se pueden formar con las cifras impares? ¿Cuántos de ellos son mayores de 70.000?
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos
![]()
Si es impar sólo puede empezar por 7 u 9.

5) A una reunión asisten 10 personas y se intercambian saludos entre todos. ¿Cuántos saludos se han intercambiado?
No entran todos los elementos.
No importa el orden.
No se repiten los elementos
![]()
6) Con las cifras 1, 2 y 3, ¿cuántos números de cinco cifras pueden formarse? ¿Cuántos son pares?
Sí entran todos los elementos: 3 < 5
Sí importa el orden.
Sí se repiten los elementos
![]()
Si el número es par tan sólo puede terminar en 2.
![]()
7) ¿De cuántas formas pueden colocarse los 11 jugadores de un equipo de fútbol teniendo en cuenta que el portero no puede ocupar otra posición distinta de la portería?
Disponemos de 10 jugadores que pueden ocupar 10 posiciones distintas.
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.
![]()
8) Una mesa presidencial está formada por ocho personas, ¿de cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?
Se forman dos grupos el primero de 2 personas y el segundo de 7 personas, en los dos se cumple que:
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.
![]()
9) Un grupo, compuesto por cinco hombres y siete mujeres, forma un comité de 2 hombres y 3 mujeres. De cuántas formas puede formarse, si:
A) Puede pertenecer a él cualquier hombre o mujer.
![]()
B) Una mujer determinada debe pertenecer al comité
![]()
C) Dos hombres determinados no pueden estar en el comité.
![]()
10) ¿Cuántos números impares de cinco cifras se pueden escribir con las cifras 1, 2, 3, 4 y 5 sin repetir ninguna cifra?
Para averiguar si se trata de variaciones, permutaciones, etc, debemos hacer las siguientes preguntas:
1ª ¿Afecta el orden?
Sí, ya que, por ejemplo, 12345 es diferente de 21345.
Por tanto puede tratarse de variaciones o permutaciones.
2ª ¿Intervienen todos los elementos en todos los grupos que se pueden formar?. Si, ya que según el enunciado del problema los cinco números siempre se utilizan en cada uno de los números.
Luego se trata de permutaciones.
3ª ¿Se pueden repetir los elementos?
No, pues según el enunciado del problema las cifras deben ser distintas.
Conclusión: Se trata de permutaciones ordinarias de 5 elementos.
Una vez que hemos averiguado que se trata de permutaciones ordinarias, veremos cuántos números diferentes de cinco cifras se pueden formar en total:
P = 5! = 5 · 4 · 3 · 2 · 1 = 120
Ahora buscaremos los que son pares, es decir, los que terminan en 2 y en 4, para lo cual tendremos en cuenta la cifra que ocupa el último lugar (2 ó 4) ya no se pueden tomar, por lo que quedan cuatro números y cuatro lugares.

Por tanto los impares son: 120 – 48 = 72
Hay 72 números impares.
11)
a) Con los números 0, 1, 2, 3, 4 y 5, cuántos números de 4 cifras se podrán hacer.
b) Cuántos acaban en 5.
c) Cuántos son mayores de 4000.
Solución:
a) Debemos tomar cuatro números de entre los dígitos 0, 1, 2, 3, 4 y 5.
Para averiguar si se trata de variaciones, permutaciones, etc, debemos hacer las siguientes preguntas:
1ª ¿Afecta el orden?
Sí, ya que, por ejemplo, 1234 es diferente de 4321.
Por tanto puede tratarse de variaciones o permutaciones.
2ª ¿Intervienen todos los elementos en todos los grupos que se pueden formar?
No, ya que tenemos seis dígitos y únicamente escogemos 4.
Luego se trata de variaciones.
3ª ¿Se pueden repetir los elementos?
Si, pues el enunciado del problema no especifica que las cifras deban ser distintas.
Conclusión: Se trata de variaciones con repetición de 6 elementos de orden 4, pero en este caso debemos tener en cuenta que los números que comienzan por cero no son de cuatro cifras, sino de tres, por tanto tendremos que restar del total de números que se pueden forma con cuatro cifras los que tienen un cero delante y por tanto son de tres cifras (el primer lugar está ocupado por el cero, luego quedan tres plazas libres por lo que serán variaciones con repetición de 6 elementos de orden 3)

